因为最近要用命名实体识别,查看论文最火热的就是LSTM+CRF 框架了,于是不可避免的要学习一下LSTM
现在这里提前膜拜一下colah大佬
为什么要用LSTM?
LSTM(Long Short Term Memory) 首先他是一种特殊的RNN。作为一个变种,那么意味着他一定解决了普通RNN没法做到的事情。所以先让我们看看普通的循环神经网络问题所在。
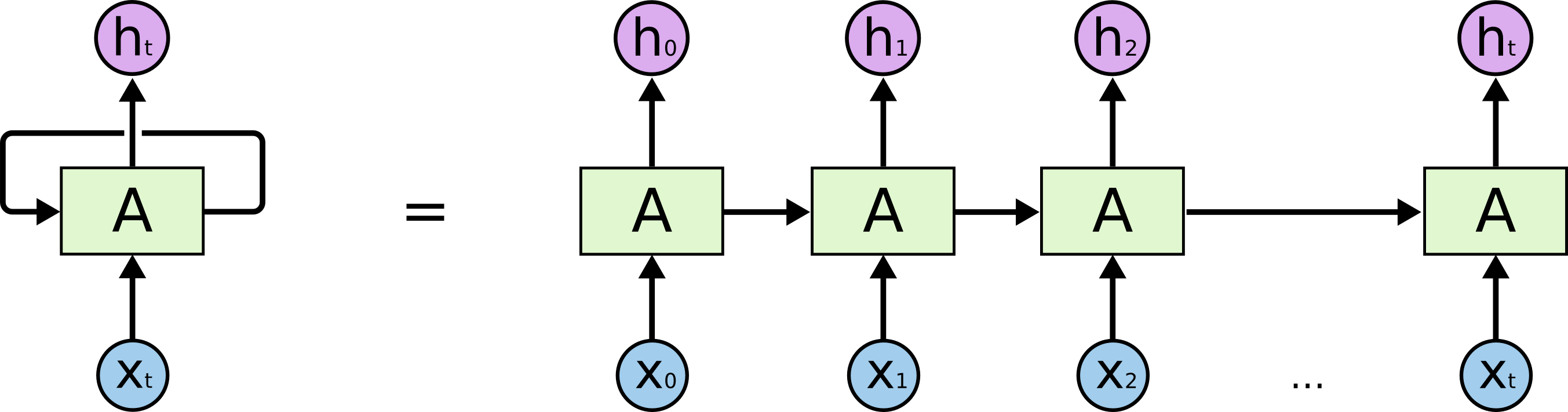
如上图所示就是一个最为普通的循环神经网络。他和一般的神经网络的区别在于:他在同一层隐藏层中,前一个神经节点的输出会作为下一个神经节点的一个输入。这就使得不同阶段的输入(如x0,x1)之间产生了关系,这种关系表现为前后关系,上下文关系或者更一般的讲叫做时间关系! 这使得神经网络的输入不再独立,而是能够进行不同时间段的联系,比较具有代表的就是语音识别、翻译等。
那么普通循环神经网络的缺点在哪里?
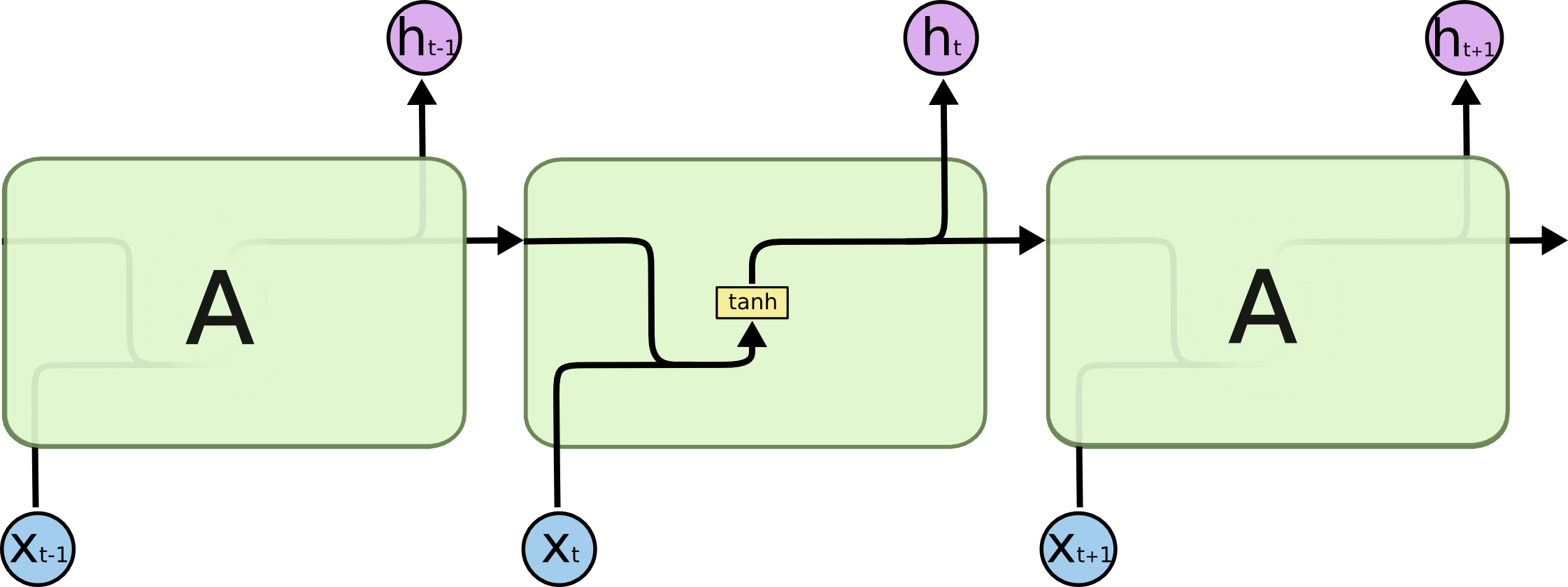
其缺点就在于他是短期记忆(Short Term)。从上图中我们可以看到,“历史信息”是会被作为输入不断的被计算的,也就意味着会被不断的稀释,而事实上经过3,4个神经节点之后,之前的信息基本上已经可以完全忽略了! 这我们当然不乐意了,我们当然希望能过记的越久越好,所以LSTM就诞生了!
LSTM如何解决长时记忆?
首先让我们看一下,LSTM的结构:
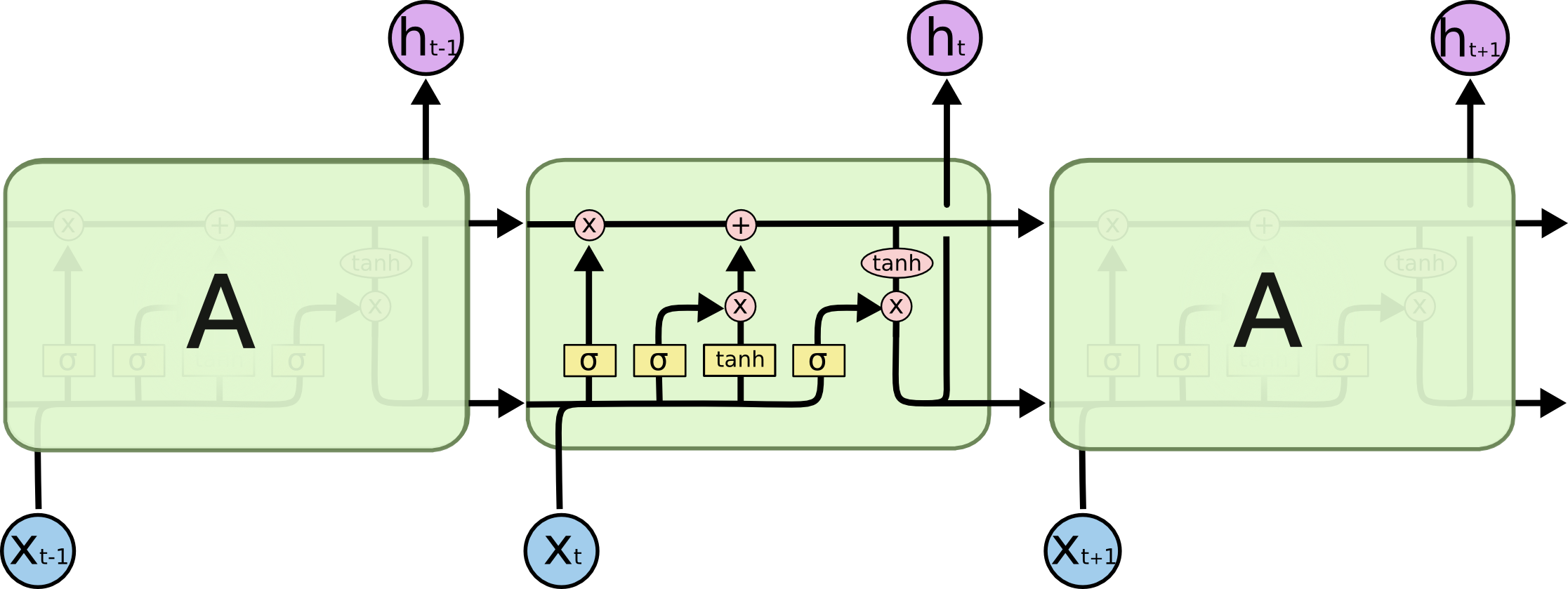
嗯。。。。看起来挺复杂的样子,将原先单一的tanh用一大堆运算进行了替代。但仔细分析一下结构,会发现其实很简单,十分符合人们解决问题的思路。
0.状态保存层
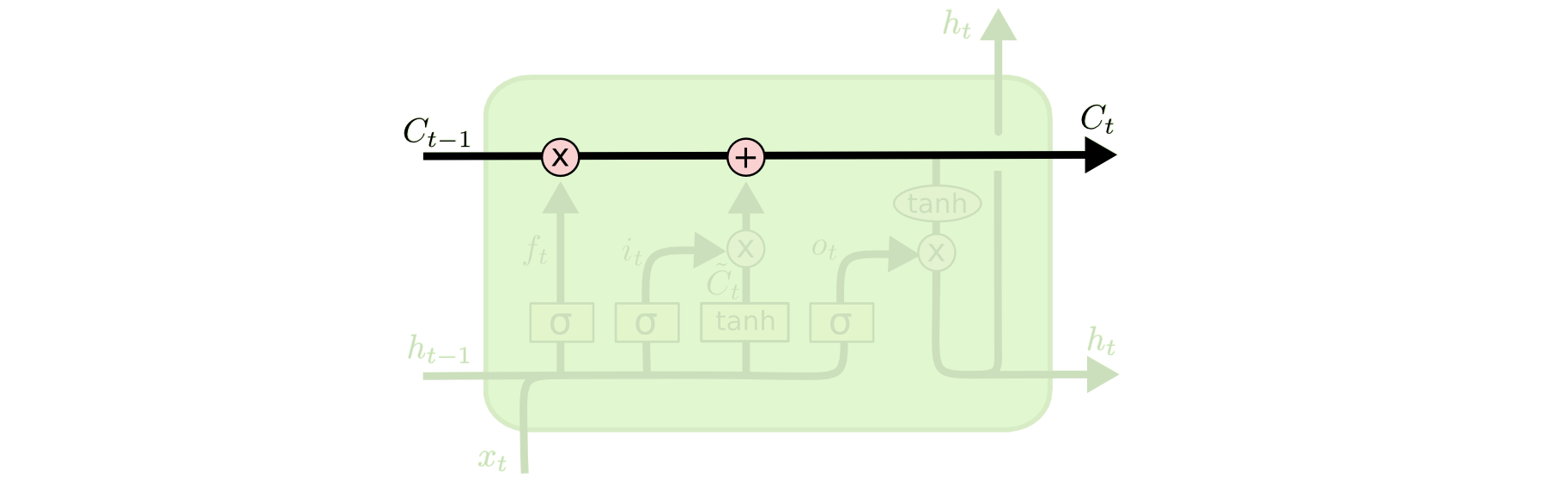
Cell State ,细胞节点状态的保存可以说是LSTM的关键所在!
前面提到了,普通RNN的历史信息会随着计算迅速消失,那么为了解决这个问题,我们要不就干脆把“历史状态”进行独立的存储。于是就出现了如图中“运输链”一般的结构,这使得信息能够长时间的保留!
1.遗忘门层 forget gate layer
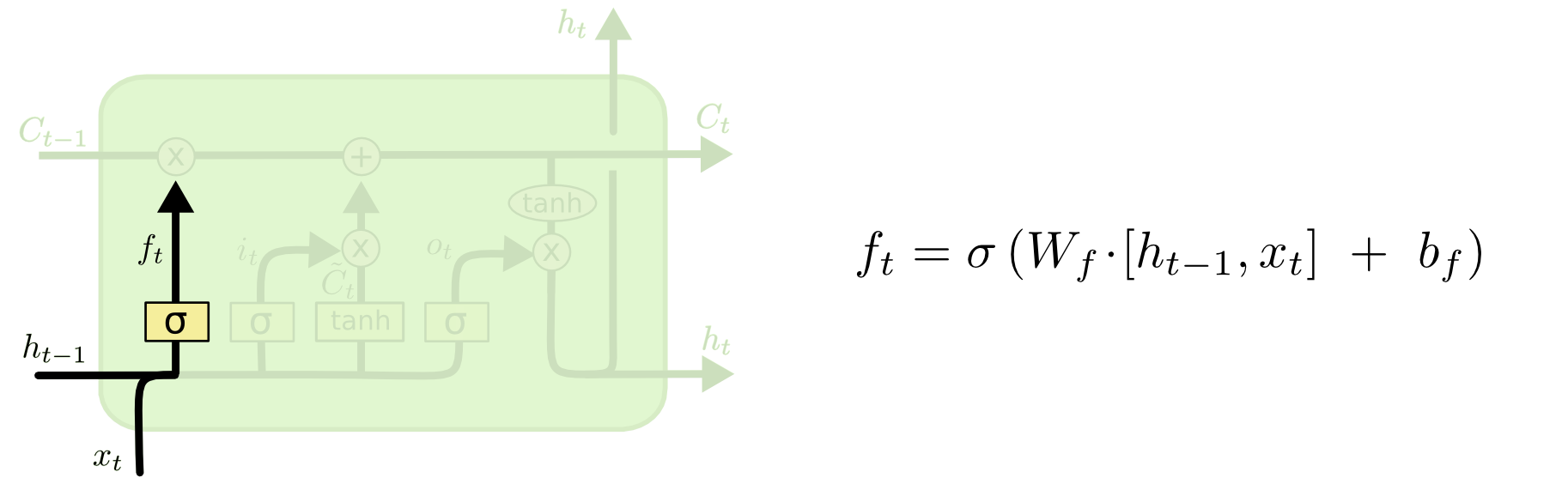
该层的作用是:生成遗忘矩阵 。
其对前一节点输出和当前节点输入进行sigmoid 处理,这样就得到了一个值介于0~1的矩阵。0表示彻底遗忘,1表示完全保留。
2.添加层
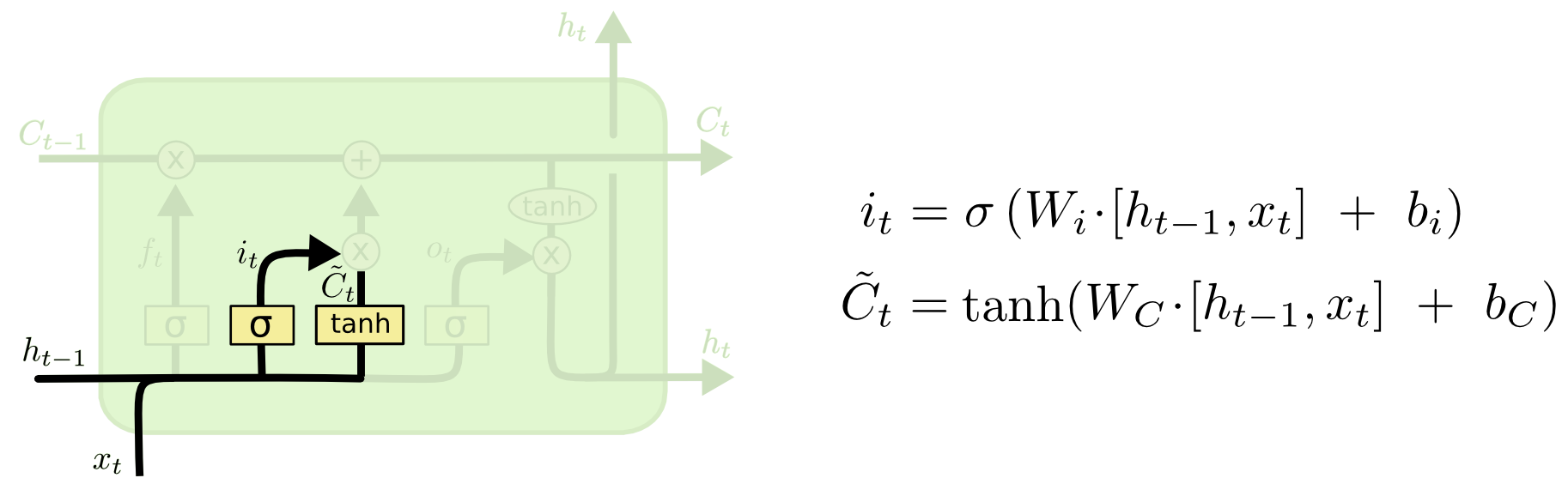
该层的作用是:生成添加矩阵。
这一层由两个部分组成:
input gate layer : 通过sigmoid函数,生成(0~1)矩阵。表示将要更新哪些值。
tanh layer : 通过tanh函数,生成(-1~1)矩阵。表示新生成的候选值。
3.状态修改层
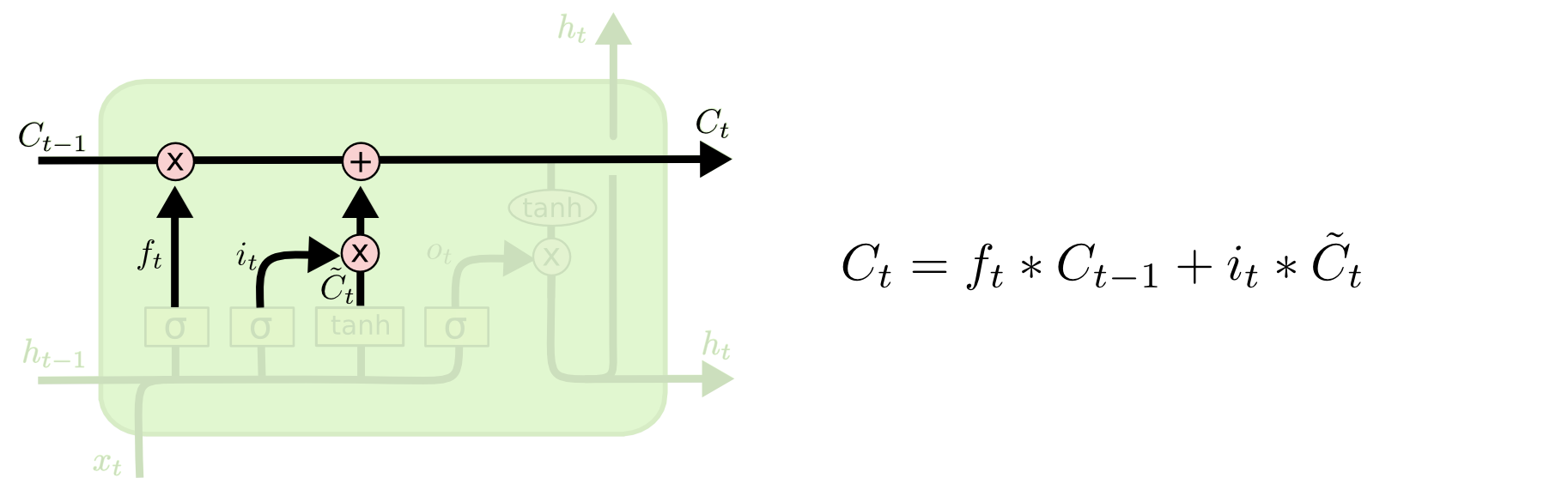
该层的作用是:修改状态
前面已经得到了遗忘矩阵和添加矩阵,那么现在只需要用状态矩阵乘以遗忘矩阵,就能遗忘相应内容;用状态矩阵加上添加矩阵,就能添加相应内容。
这样状态既能长久保存,又能随着时间进行修改。
4.输出层
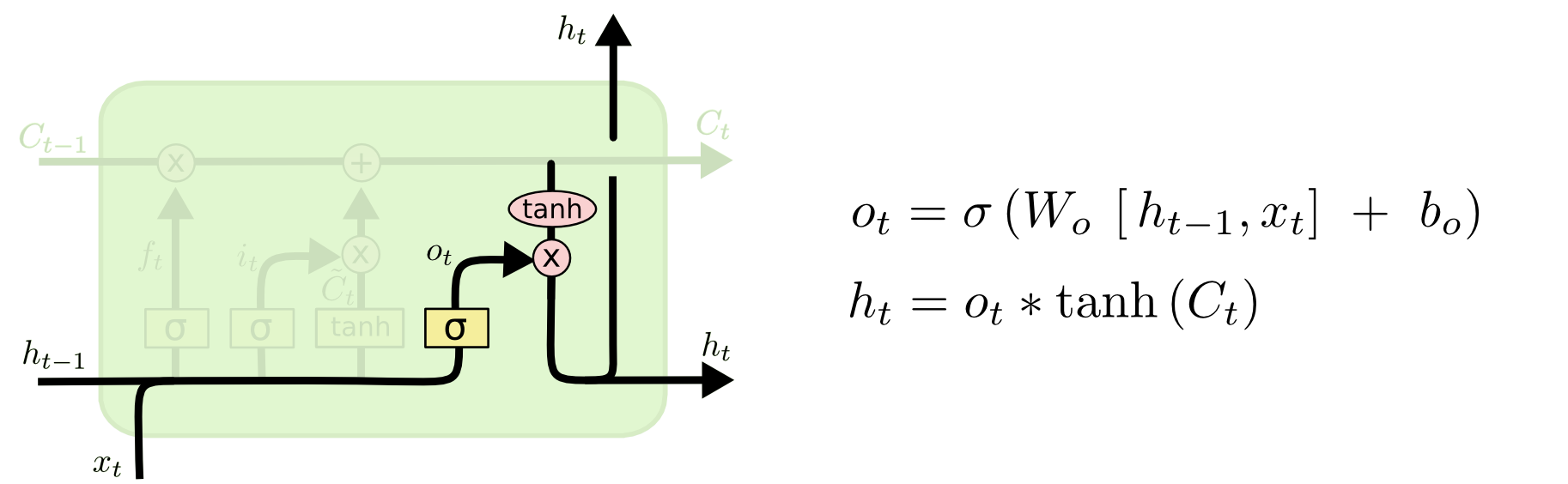
输出层也分为两个部分:
input gate layer : 通过sigmoid函数,生成(0~1)矩阵。表示输入的特征分布。
tanh layer : 通过tanh函数,生成(-1~1)矩阵。表示已经学得的历史状态。
然后两者相乘,就得到了在历史中,遇到这种输入时的输出情况!
5. 总结
从上面的过程中可以体会到LSTM的几点本质:
- 所谓状态的保留,实际上保留的是之前出现的各种情况!最后状态矩阵可以看成数据整体的分布关系矩阵。
- sigmoid函数,生成(0~1)矩阵类似一个门(gate)。表示了数据关系的特点,嗯主要还是便于相乘得到结果。
- tanh函数,生成(-1~1)矩阵。表现了数据关系分布的状况。
LSTM的变种
很明显,LSTM的核并不是唯一的,只要大致的思路一致,那么轻微的变化都是可以的。
1.peephole connections
Gers & Schmidhuber (2000)。将状态也作为gate层的输入。
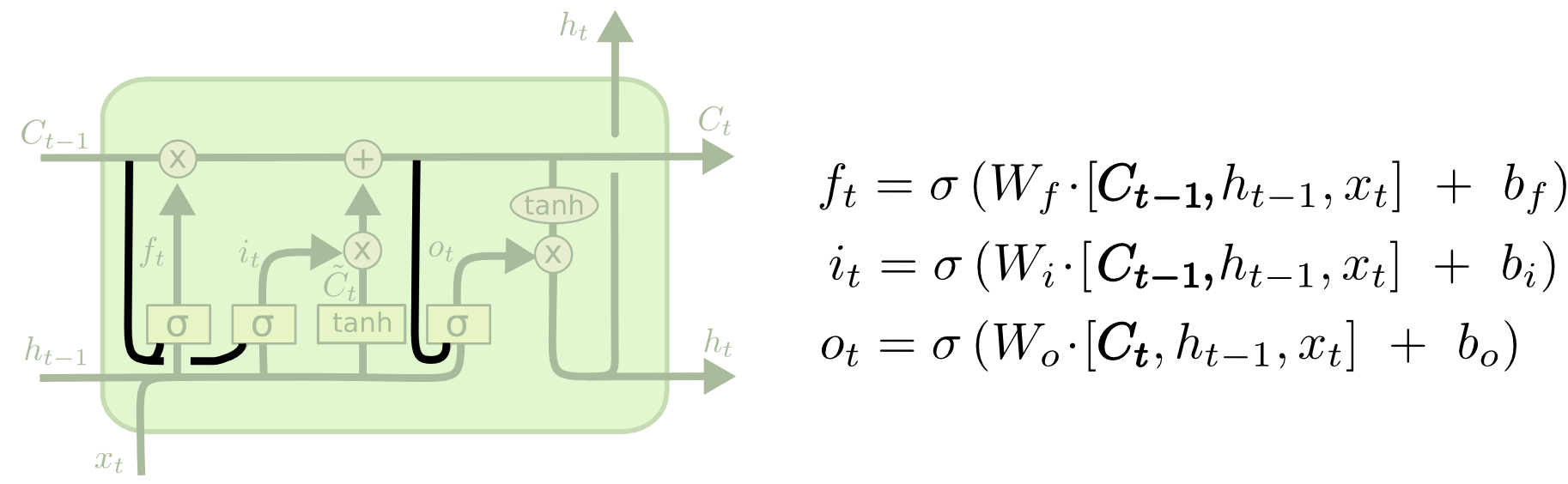
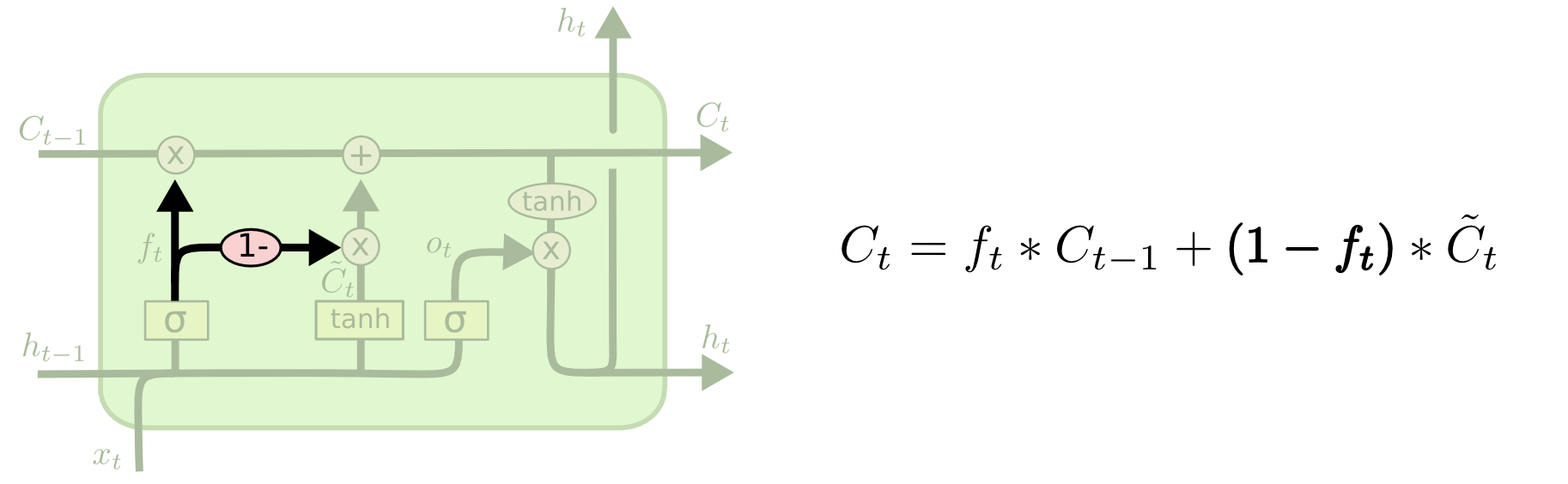
2.coupled forget and input gates
将遗忘层和添加层进行耦合,不再独立。
3.GRU(Gated Recurrent Unit)
Cho, et al. (2014). 非常常用的模型,几乎可以替代LSTM。他把forget,input gate合并成了“updata gate”,通过“reset gate”生成$\widetilde{h}$ ,抛弃了memory cell,由于参数变少(LSTM需要训练8个参数矩阵,而GRU只需要训练3个)使得该模型可以比LSTM训练的更快,而且由于公式简单使得GRU修改起来也方便,最重要的是训练结果没有什么差别!!

4.总结
还有其他许多LSTM变种,其实只要思路一致,(反正训练都是凑参数),都是能够得到相似结果的。
如Greff, et al. (2015)实验发现这些模型最后的结果基本上都一样。
LSTM、GRU为什么能够解决梯度消失?
注意!!梯度消失在DNN和RNN中意义不一样 。DNN中梯度消失指的是误差无法传递回浅层,导致浅层的参数无法更新;而RNN中的梯度消失是指较早时间步所贡献的更新值,无法被较后面的时间步获取,导致后面时间步进行误差更新的时候,采用的只是附近时间步的数据。
LSTM和GRU能够解决梯度消失的主要原因在于更新状态矩阵的方式:$C_t = f_tC_{t-1}+i_t\tilde{C}_t$ 和 $h_t = (1-z_t)h_{t-1}+z_t\tilde{h}_t$ 它们采用了线性运算,仔细一看这不类似短连接、残差结构吗?这使得求导值不会太小,有效减小了梯度消失问题。一般20个词左右。