SVM | CLD的博客

　　支持向量机(Support Vector Machine,SVM)，作为一个优秀的分类算法，不管用不用学习一下是必须的。不过说实话，SVM的原理很简单，但证明却很难。如果只是想用一下SVM，调用一下已实现的库（scikit-learn），调调参数还是很容易的。所以作为一个数学渣，这里不会涉及详细的推导，只是尽可能简单的去理一遍整个推导过程（当然重要的公式是少不了的）。如果要学习一下详细的推导过程可以看一下刘建平大佬的博客。

SVM的直观理解

　　首先作为一个二分类器，目标很简单：把数据分为两类，也就是找一条分割线、平面、超平面。

那么问题是，以什么标准去找这个超平面？

　　现在给你一堆数据，让你去寻找一个超平面去分割两类数据。这个时候往往会有很多种分法（如下图所示），但是很明显我们需要一条泛化能力强的分割线，来适应后续增加的数据。那么，很自然的，我们会把这个分割线尽可能的远离两类数据，尽量使的分割线处于中间（我离你们远一点总不会错吧~）。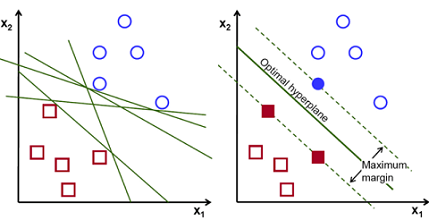

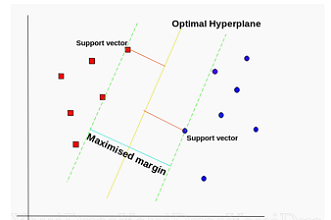
　　SVM就是这么干的，SVM从几何的角度出发，力求寻找一个离两个类一样远的超平面，并且离的还要尽可能的远！而每个类中离超平面最近的点叫做支持向量（Support Vector） 。好吧，支持向量机的名字就是这么来的，大概就是通过这些“支持向量”得到了这个分类器（机）吧~

SVM的直观数学表达

首先假设目标超平面

　　　　 $\omega^Tx+b=0$

空间任意点到超平面的距离为

　　　　 $r=\frac{|\omega^Tx+b|}{||\omega||}$

假设两个与目标超平面平行的超平面,并通过“支持向量”

　　两个超平面为： $\omega^Tx+b=-1$ 和 $\omega^Tx+b=1$，（这里取1，-1是为了后续计算方便）

　　因为数据都在这两个超平面之外，于是就有了

　　　　 $\omega^Tx+b\le-1,(y_i = -1)$

　　　　 $\omega^Tx+b\ge+1,(y_i = 1)$

　　　　 => $y_i(\omega^Tx+b)\ge1,i=1,2…,m$

那么可以获得两个类的最远距离

　　　　$\gamma=\frac{2}{||\omega||}$ ,这个距离被称为间隔margin

我们的目标就是寻找最大间隔的超平面

　　即　$max_{\omega,b}\frac{2}{||w||}\quad s.t. y_i(\omega^Tx+b)\ge1,i=1,2…,m$

为了后续求解方便，重写

　　　　 $min_{\omega,b}\frac{1}{2}||\omega||^2\quad s.t. y_i(\omega^Tx+b)\ge1,i=1,2…,m$

　　这个就是SVM的基本型！

注：在推导过程中，进行了一个巧妙的假设，最近的点（支持向量）到超平面的距离为1，这个假设使得最大间隔的数学表示变的很简单，但也增加了一个不等式约束。另外注意y取值为+1和-1，也是为了计算方便。

SVM的对偶数学表达

　　我们现在的目标很清晰就是求出满足基本型的w和b

　　　　　★★ $min_{\omega,b}\frac{1}{2}||\omega||^2\quad s.t. y_i(\omega^Tx+b)\ge1,i=1,2…,m$

　　虽然这是个凸二次规划问题，有现成的包可以求解，但这里有一个更加高效的方法….

拉格朗日乘子法 & 对偶问题

　　正好有一个现成的方法可以用来解决这类不等式约束的问题，那就是拉格朗日乘子法。

　　该问题的拉格朗日函数为：$L(\omega,b,\alpha)=\frac{1}{2}||\omega||^2+\sum_{i=1}^m\alpha_i(1-y_i(\omega^Tx_i+b)),\alpha_i\ge0$

现在我们的目标变成了两个：
　　　　① 对于拉格朗日乘子α最大化L（拉格朗日乘子法要求）
　　　　② 对于ω、b最小化L（SVM要求）
　　　　即：$min_{w,b}max_{a_i\ge0} L(\omega,b,\alpha)$

　　再让我们看一下这个新函数是怎么实现约束条件的：
　　　　当不满足约束条件时，右面括号里面的值将大于0，这个时候求max是不存在的。
　　　　当满足约束条件时，先求max，公式右边必将为0，那么求min时就变为了求$\frac{1}{2}||\omega||^2$的原问题。

　　整个约束条件即为KKT(Karush-Kuhn-Tucker)条件：

　　　　 $\begin{equation} \begin{cases}\alpha_i\ge0; \\y_if(x_i)-1\ge0;\\ \alpha_i(y_if(x_i)-1)=0. &\end{cases}\end{equation}$　　

　　从这个条件我们可以看出一个问题：只有支持向量的α存在非0值，其他样本的α必将取0！

　　再看，如果我们先求max，α的个数比较多且是不等式约束不好求，所以在满足KKT条件下转为对偶问题：
　　　　 $max_{a_i\ge0} min_{w,b} L(\omega,b,\alpha)$

求解对偶问题

　　首先求解L基于ω和b的极小值，直接求偏导为0：

　　　　$\omega=\sum_{i=1}^m\alpha_iy_ix_i$

　　　　 $0=\sum_{i=1}^m\alpha_iy_i$

带入原式得到只关于α的极大值问题：

　　　　 ★★ $max_\alpha \sum_{i=1}^m\alpha_i-\frac{1}{2}\sum_{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy_iy_jx_i^Tx_j\quad s.t. \sum_{i=1}^m\alpha_iy_i=0,\alpha_i\ge0$

　　通过SMO(Sequential Minimal Optimization)算法获得α值，即可获得最终模型：

　　　　 ★★ $f(x)=\omega^Tx+b=\sum_{i=1}^m\alpha_iy_ix_i^Tx+b$

SMO算法

　　SMO（序列最小优化）算法是一种启发式的方法，其关键在于利用了$0=\sum_{i=1}^m\alpha_iy_i$这个等式。
　　SMO算法每次只优化两个变量，将其他的变量都视为常数，这样就从多变量的优化问题变成了两变量的优化问题。再加上等式的存在，使得这两个变量可以互相表示，这样一来问题近一步简化为了单变量二次规划问题。这样一来就能很容易的优化α值。

　　那么怎么选取每次优化的两个α值？
　　已证明[Osuna et al., 1997]，只需选取的α中有一个不满足KKT条件，目标函数就会在迭代后增大。
　　所以我们选取α的策略是：
　　　　 ① 先选取一个违背KKT条件程度最大的变量。
　　　　 ② 选取的第二个变量与第一个变量对应样本之间的间隔最大（最大化步长）。这样有助于加快优化。

b值求解

　　求导之后我们发现b不见了，好在对于任意的支持向量都有$y_sf(x_s)=1$

　　　即：$y_s(\sum_{i\in S}\alpha_iy_ix_i^Tx_s+b)=1,S为所有支持向量的下标$

　　为了结果更鲁棒，b使用所有支持向量的平均值：

　　　　 ★ $b=\frac{1}{|S|}\sum_{s\in S}(1/y_s-\sum_{i\in S}\alpha_iy_ix_i^Tx_s)$

总结： 我们通过一系列的优化手段，最终获得了一个只与α有关的单变量模型：

　　　 $f(x)=\omega^Tx+b=\sum_{i=1}^m\alpha_iy_ix_i^Tx+b$

　　这个模型有一个特点：只有支持向量拥有非0的α！这也造成了SVM的一个重要性质：训练完成后，大部分的训练样本都不需要保留，最终模型只与支持向量有关！

核函数

　　上面讲了那么多，一直在讲线性可分问题，但是现实任务往往是线性不可分的。但好在，如果原始空间是有限维，即属性数有限，那么一定存在一个高维特征空间使样本可分！

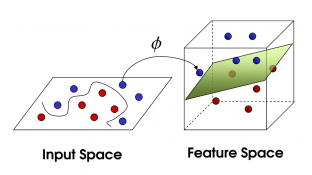
我们尝试对原数据进行映射Φ(X)

　　　　$f(x) = \omega^T\phi(x)+b$

　　经过一系列变换之后得到对偶问题：

　　　　$max_\alpha \sum_{i=1}^m\alpha_i-\frac{1}{2}\sum_{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy_iy_j\phi (x_i)^T\phi (x_j)\quad s.t. \sum_{i=1}^m\alpha_iy_i=0,\alpha_i\ge0$

　　如果直接求解因为要计算$\phi (x_i)^T\phi (x_j)$，这是样本映射到特征空间之后的内积，而特征空间可能维度很高甚至无穷维，通常无法直接运算。

设想有这样一个函数：

　　　　 $k(x_i,x_j)=\phi (x_i)^T\phi (x_j)$

　　也就是说在特征空间的内积等于它们在原始样本空间中通过函数k(.,.)计算的结果。

　　这个函数K就是核函数(kernel function)！

　　这种将内积替换为核函数的方式称为核技巧（kernel trick）

　　有定理证明：只要一个对称函数所对应的核矩阵半正定，它就能作为核函数使用。

常用核函数

名称	表达式	参数
线性核	$k(x_i,x_j)=x_i^Tx_j$
多项式核	$k(x_i,x_j)=(x_i^Tx_j)^d$	d>=1为多项式次数
高斯核,RBF核	$k(x_i,x_j)=exp(-\frac{abs(x_i-x_j)^2}{2\sigma^2})$	σ>0为高斯核宽度
拉普拉斯核	$k(x_i,x_j)=exp(-\frac{abs(x_i-x_j)}{\sigma})$	σ>0
Sigmoid核	$k(x_i,x_j)=tanh(\beta x_i^Tx_j+\theta)$	双曲正切函数，β>0,θ<0

　　 注意：核函数的选择是SVM中最大的变数，因为你并不知道具体会怎么映射。
　　高斯核可以映射到一个无穷维的空间，所以理论上可以分类各种数据。

带核函数的最终模型

　　 ★★ $f(x)=\omega^Tx+b=\sum_{i=1}^m\alpha_iy_ik(x,x_i)+b$

　　对比之前的最终模型发现：$k(x,x_i)=x_i^Tx$ ,嗯可以认为原来的模型用了线性核~

软间隔

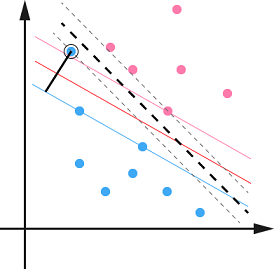
　　前面我们总是找一个超平面将数据完全分开，就如图中的黑色超平面一样。但是现实数据是有噪声的会有异常值。如果有异常值被当做了支持向量来确定超平面，那么这个超平面的泛化能力一定不会好（过拟合），所以我们需要对这种异常值有一定的容忍能力。
　　硬间隔（hard margin）： 间隔中不存在样本，即所有样本都划分正确。
　　软间隔（soft margin）： 允许间隔中存在一定的样本，即不要求所有样本都划分正确。

添加惩罚

　　既允许不满足约束的点存在，又要这些点尽可能的少，那么可以通过添加惩罚的方式来约束这些点。

　　优化目标变为: $min_{\omega,b} \frac{1}{2}||\omega||^2+C\sum_{i=1}^m\ell(y_i(\omega^Tx_i+b)-1)$

　　其中C为惩罚参数，C越大，对误分类的惩罚越大，C越小，对误分类的惩罚越小。

　　其中ι为替代损失（surrogate loss），常见的替代损失函数有：

　　　　★ hinge 损失（合页损失）： $\ell(z)=max(0,1-z)$

　　　　● 指数损失（exponential loss）：$\ell(z)=exp(-z)$

　　　　● 对率损失（logistics loss）：$\ell(z)=log(1+exp(-z))$

　　其中hinge损失函数是最常用的（scikit-learn中就使用这种损失函数），一般讨论SVM时就默认这种损失函数。

松弛变量

　　为了书写、表达方便，使用松弛变量（slack variable）来表示损失值：

　　　　 $min_{\omega,b,\xi_i} \frac{1}{2}||\omega||^2+C\sum_{i=1}^m\xi_i\quad s.t. y_i(\omega^Tx_i+b)\ge1-\xi_i\quad \xi_i\ge0,i=1,2…m$

　　每个样本都有一个对应的松弛变量，用来表征样本不满足约束的程度，是样本到超平面距离的一个度量。

　　可以看到原来的约束是：$y_i(\omega^Tx_i+b)\ge1$ ，即点必须都在间隔之外。
　　现在变成了$y_i(\omega^Tx_i+b)\ge1-\xi_i$ , 可以看成允许到间隔内了。以hinge为例，$z+max(0,1-z)\ge$1 ，z无约束。也就是说hinge允许样本在任何地方，只是对间隔内的样本进行了惩罚！！这个时候边界周围的点都是支持向量（当然分错的更是，因为这些点拥有非0的ξ，α值。一般支持向量会在超平面附近聚集成团）！！

参数求解

　　求解流程和之前完全一致，当求解对偶问题时：

　　　　 $max_\alpha \sum_{i=1}^m\alpha_i-\frac{1}{2}\sum_{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy_iy_jx_i^Tx_j\quad s.t. \sum_{i=1}^m\alpha_iy_i=0, 0\le a_i\le C$

　　和原来没有太大的差别，只是α的取值范围发生了变化。

　　最终模型样式没有什么变化：

　　　　 $f(x)=\omega^Tx+b=\sum_{i=1}^m\alpha_iy_ix_i^Tx+b$

从损失函数角度看SVM

　　SVM的损失函数可以写成：

　　　　 $min\frac{1}{2}||\omega||^2+C\sum_{i=1}^m\ell(f(x_i),y_i)$

　　左边的这项是不是很像正则化的L2范数？没错，这项称为结构风险（structural risk）：用于描述模型的某些性质。以贝叶斯估计的角度来看，这提供了模型的先验概率。比如L2范数倾向于参数尽量均匀，L0和L1范数则倾向参数尽量稀疏。

　　右边一项则像模型训练时计算得到的误差。这项称为经验风险（empirical risk）：用于描述模型与训练数据的契合程度。

　　C则是两者的一个权重比。

　　这个时候，你可能会想，那要是我把L这个损失函数换一换不就可以得到各种不同的模型了？比如把损失函数替换成对率损失函数，你会发现几乎得到了逻辑回归！两者的性能也相当！所以这体现了SVM的强大！

　　整个模型可以看成：核函数拟合空间，软间隔设置损失函数，$\omega^2$ 作为L2正则项。 非常完整，理论上能够轻松模拟其他的模型！

SVM调参

　　SVM由libsvm进行了实现，而scikit-learn底层调用了libsvm，那么当然是用功能更全的scikit-learn来进行SVM训练啦。

整体流程

对数据做归一化（simple scaling），因为SVM是通过距离来估计的，是否归一化会有较大影响。
看是否为多分类，并选择decision_function_shape = ‘ovo’ or ‘ovr’
看数据是否strongly unbalance，并选择class_weight = ‘balanced’ or ‘自定义比例’
看是否最后需要得到概率值，并选择probability = True or Flase
根据情况选择 without kernel 还是 RBF kernel
通过 cross-validation 和 grid-search 得到最优的 C 和 gamma

参数意义

　　一般做SVM都是用RBF kernel，所以如何获得一个好的 C 和 gamma成为了关键。

　　C（默认为1）：惩罚系数，权重，即对误差的宽容度。C 越高，说明越不能容忍出现误差,容易过拟合。C 越小，容易欠拟合 。

　　gamma$\frac{1}{2\sigma^2}$（默认为1/特征数）：决定了高斯核的宽度，决定了单个样例有多少影响力。gamma越大则函数越陡，意味着这个样例能够影响越多的周围样例，也就意味着样例之间的关系更为的紧密，而训练时过度的关注样例之间的关系往往会造成过拟合，反之gamma越小，样例之间的关系越弱，往往会造成欠拟合 。

　　支持向量：支持向量越多，意味着模型对训练数据越信任，模型也越复杂，容易发生过拟合，反之同理。为什么我要在这里提到支持向量？因为很多人喜欢从C、gamma去推断支持向量的变化再去推断模型学习的情况，但我个人认为这样并不好，虽然从结果看是这么一回事，但我觉得去推支持向量是个不明智的选择，支持向量更像是模型训练时的选择，通过支持向量再来理解反而自己难为自己，还不如直接去推断（当然可能是因为我的理解能力不够~）。

　　从实验的结果来看，C越大，gamma越大，支持向量就越多，容易发生过拟合。
　　　　　　　　　　　C越小，gamma越小，支持向量就越少，容易发生欠拟合。

具体调参

　　通过 cross-validation 和 grid-search 得到最优的 C 和 gamma 。
　　在scikit-learn中通过sklearn.model_selection.GridSearchCV 实现。

from sklearn.grid_search import GridSearchCV    
from sklearn.svm import SVC   
from sklearn.preprocessing import StandardScaler
true# 对数据进行归一化
truetrain_x = StandardScaler.fit_transform(train_x)
    # probability:允许后续概率形式输出
    model = SVC(kernel='rbf', probability=True)    
    param_grid = {'C': [1e-3, 1e-2, 1e-1, 1, 10, 100, 1000], 'gamma': [0.001, 0.0001]} 
    # cv=n折交叉验证，更多参数见文档
    grid_search = GridSearchCV(model, param_grid, cv = 5)    
    grid_search.fit(train_x, train_y)    
    best_parameters = grid_search.best_estimator_.get_params()  
    model = SVC(kernel='rbf', C=best_parameters['C'], gamma=best_parameters['gamma'], probability=True)    
    model.fit(train_x, train_y)

SVM VS LR

　　在上面我们已经发现，两者的损失函数十分像，当SVM采用对率损失函数时就根本没有差别了。

相同点

都是二分类算法
都是监督学习
都是判别式

不同点参考了Drakos

一般svm使用hinge损失函数，这样一来，SVM一般会比LR稍微好一点。
svm通过最大化间隔来寻找超平面，而LR通过分类概率来寻找超平面。这使得svm的结果尽可能的远离两个类，而LR的结果没有这个性质。

svm对于异常值没有LR敏感，因为逻辑回归的损失函数更敏感。

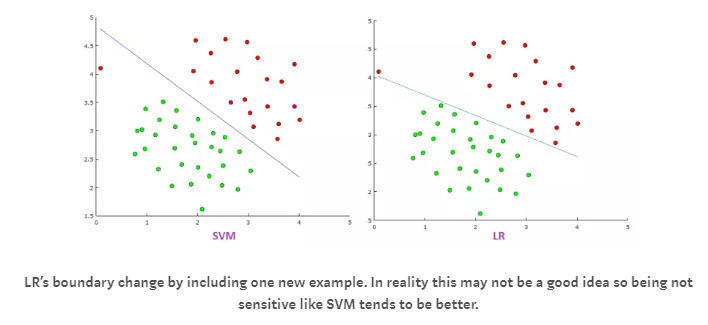
svm的输出是0或1，而LR的输出是一个概率。这使得在某些时候LR的解释性更强。当然也有后续的办法使得svm输出概率。
Linear SVM依赖数据表达的距离测度，所以需要对数据先做normalization；LR不受其影响。
LR受所有数据点的影响，SVM则只受支持向量的影响。如果数据不同类别strongly unbalance，LR相比SVM更受影响，一般都需要先对数据做balancing。

什么时候使用SVM? LR? NN?