通过算法学习,我们可以得到数据的模型,但我们应该怎么评估这个模型好坏,怎么与其他模型比较?
1.误差与拟合
错误率 error rate:分类错误的样本数占总样本的比例。
精度 accuracy: 1-错误率。
误差 error:更一般的、实际预测输出与真实输出之间的差异 。
训练误差 training error 、经验误差 empirical error:在训练集上的误差。
泛化误差 generalization:在新样本上的误差。
毫无疑问,我们的目标当然是使泛化误差尽可能小。但我们并不知道新样本会是什么
(如果知道就用来训练了),因此实际中我们只能尽可能的使训练误差减小。
过拟合 overfitting: 在训练集上表现很好,但在实际使用中泛化性能不佳。
欠拟合 underfitting : 连训练集上都未学习好。
欠拟合相对比较容易克服,多训练几轮就可以了。
但过拟合却十分麻烦!机器学习的问题往往是NP难问题,简单的说就是无法在多项式时间内获得最优解,只能获得一个近似、局部最优解。这个解会尽量使训练误差最小,这就会导致模型过度的学习训练样本,将样本的一些自身特点当做了一般特性,这就导致了过拟合。因为无法获得全局最优解,因此过拟合是无法避免的!
2.评估方法
从上面对过拟合的分析我们知道光看训练误差是没有什么意义的,我们需要知道泛化误差,来帮助我们进行模型选择(model selection)和调参(parameter tuning)。为了能够评估泛化误差,我们需要一个测试集(testing set)来模拟新样本。那么这个测试集从哪里来?
😄 为了与实际遇到的真实测试数据进行区别,测试集常被称为验证集(validation set) 。
留出法 hold-out
简单暴力,直接将数据集划分为两个互斥的集合,一个作为训练集,一个作为测试集。
注意一:划分时要尽可能保持数据分布的一致性,可以使用分层采样(stratified sampling)的方式。
注意二:由于存在多种划分方式,因此一般进行多次随机划分然后对每次结果取平均值。
注意三:测试集小,会导致评估结果方差较大(过拟合);训练集小,会导致评估结果偏差较大(欠拟合)。一般将2/3~4/5的数据作为训练集,而测试集一般至少应含30个样例。
交叉验证 cross validation
将数据集划分为K个大小相似的互斥子集。每个子集尽量保持数据发布的一致性(分层抽样)。然后每次用K-1个子集作为训练集,剩下那个子集作为测试集,这样就可以进行K次训练和测试,最后返回均值。
因为分为 K个,因此又称为“K折交叉验证”、“K倍交叉验证”。K一般取10左右。
当K取样本大小时,则称为:留一法(Leave-One-Out,LOO),这种评估结果往往认为比较准确,但是计算开销实在太大。
又由于存在多种划分方式,因此通常要随机使用不同的划分方式重复P次,最终结果为这p次K折交叉验证结果的均值。
自助法(可重复采样、有放回采样) bootstrapping
上面的两种方法,都会导致训练集小于数据集,这会产生评估偏差,而自助法能够解决这个问题。
自助法以自助采样法为基础。给定包含m个样本的数据集D,采用生成数据集D‘:每次从D中随机取一个样本放入D’,并放回D,使D始终不变。重复m次后,就会获得包含m个样本的数据集D‘。我们可以估计一下D中未被采样到的样本数:$(1-1/m)^m$取极限约为0.368。这意味着有36.8%的数据未被采样到。于是我们将D’作为训练样本,D\D’作为测试样本,这样我们的训练集大小任为m,在这方面不会引入评估偏差。
注意!自助法在数据集较小,难以有效划分训练\测试集时很有用。
但当数据集足够大时,留出法和交叉验证法更常用。因为自助法会改变数据集发布,也会引入偏差。
3.性能度量
在上面评估方法中对于数据集的度量使用的是泛化误差。但在实际使用中只使用泛化误差往往是不够的,我们需要更为全面的性能度量标准。
3.1混淆矩阵(confusion matrix)
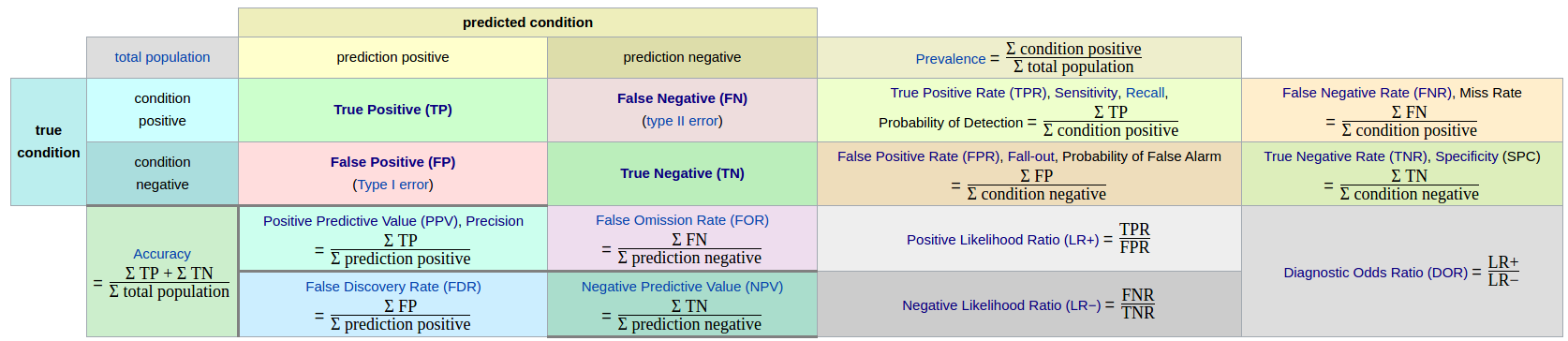
True、False:预测的结果是否正确 Positive、Negative:预测的结果
混淆矩阵通过不同的组合可以形成这种参数指标
1.正确率 precision
$Precision=\frac{TP}{TP+FP}$
2.真阳性率(True Positive Rate TPR),灵敏度(Sensitivity),召回率(Recall)
$Sensitivity=Recall=TPR=\frac{TP}{TP+FN}$
3.真阴性率(True Negative Rate TNR),特异度(Specificity)
$Specificity=TNR=\frac{TN}{FP+TN}$
4.假阴性(False Negative Rate FNR),漏诊率
$FNR=\frac{FN}{TP+FN}$
5.假阳性(False Positive Rate FPR),误诊率
$FPR=\frac{FP}{FP+TN}$
6.阳性似然比(Positive Likelihood Ratio LR+)
$LR+ =\frac{TPR}{FPR}=\frac{Sensitivity}{1-Specificity}$
7.阴性似然比(Negative Likelihood Ratio LR-)
$LR- =\frac{FNR}{TNR}=\frac{1-Sensitivity}{Specificity}$
8.Youden 指数
$Youden index=Sensitivity+Specificity-1=TPR-FPR$
3.2查准率(Precision),召回率(Recall),F值
P值,R值,F值可以说是最为常用的指标了
$P=\frac{TP}{TP+FP}$
$ R=\frac{TP}{TP+FN}$
$F_\beta=\frac{(1+\beta^2)\times P\times R}{(\beta^2\times P)+R} (\beta>0)$
P值:预测为真且正确的样本数,占预测为真的样本数的比例。
R值:预测为真且正确的样本数,占实际为真的样本数的比例。
我们的目标当然是P值和R值越高越好,但是这两者却是矛盾的。
高R低P:宁可错杀不可放过,
只要它是那我一定说是。比如对于癌症的预测宁可误诊也不能漏诊。高P低R:宁可放过不可错杀,
我说他是那他就是。比如人道主义的判断坏人,只要判断是坏人那就一定是。
但是到底应该怎么取P,R值的大小,实在麻烦,于是就有了F值。
F值: 参数=1 F1为P和R的调和平均数,两者一样重要。
参数<1 侧重于R值
参数>1 侧重于P值
但是有时候我们会有多个混淆矩阵,比如进行了多次训练/测试。这时候我们只要对P,R,F值稍加修改就行了。
宏 macro: 先求出各个P,R值。然后求平均P,R值。最后求F值。
$macro-P=\frac{1}{n}\sum\limits_{i=1}^{n} P_i$
$macro-R=\frac{1}{n}\sum\limits_{i=1}^{n} R_i$
$macro-F_1=\frac{2\times macro-P\times MACRO-R}{macro-P+macro-R}$
微 micro:先求平均再求P,R,F
$micro-P=\frac{\overline{TP}}{\overline{TP}+\overline{FP}}$
$micro-R=\frac{\overline{TP}}{\overline{TP}+\overline{FN}}$
$micro-F_1=\frac{2\times micro-P\times micro-R}{micro-P+micro-R}$
3.3ROC与AUC
多用于度量分类算法。
优势:当测试集中的正负样本的分布变化的时候,ROC曲线能够保持不变(P-R曲线会变化明显)。
在实际的数据集中经常会出现类不平衡(class imbalance)现象,即负样本比正样本多很多(或者相反),而且测试数据中的正负样本的分布也可能随着时间变化。
ROC(Receiver Operating Characteristic)反映敏感性和特异性连续变量的综合指标,曲线上每个点反映着对同一信号刺激的感受性。
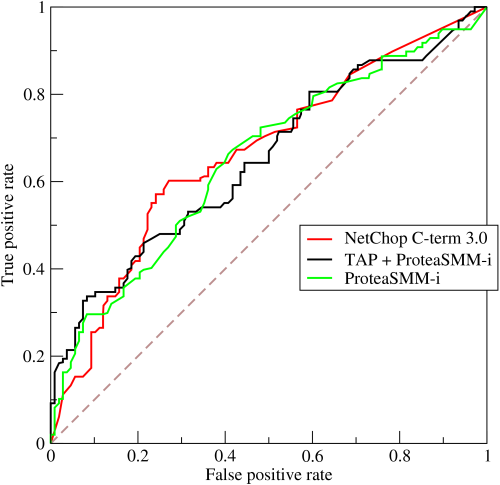
横轴: 假阳性 $FPR=\frac{FP}{FP+TN}$ 预测为正但实际为负的样本占所有负例样本的比例
纵轴: 真阳性 $TPR=\frac{TP}{TP+FN}$ 预测为正且实际为正的样本占所有正例样本的比例
对于分类器,改变最后的分类阈值,就可以获得不同大小的FPR和TPR,用于画出ROC图。
理想目标:TPR=1,FPR=0,即图中(0,1)点,故ROC曲线越靠拢(0,1)点越好。
但是往往并不能很好的判断出,两个ROC图,哪个更好,更接近(0,1)点。
于是便有了AUC。
AUC (Area under the curve)为ROC曲线下的面积,显然这个面积的数值不会大于1。又由于ROC曲线一般都处于y=x这条直线的上方,所以AUC的取值范围一般在0.5和1之间(小于0.5那么这个分类器还不如投硬币……)。AUC值越大的分类器,正确率越高。
对于AUC的计算有多种方法(参考):
1.直接计算,知道坐标{(x1,y1),(x2,y2)……(xm,ym)}
$AUC=\frac{1}{2}\sum\limits_{i=1}^{m-1}(x_i+1-x_i)*(y_i+y_{i+1})$
2.在有M个正样本,N个负样本的数据集里。一共有MN对样本(一对样本即,一个正样本与一个负样本)。统计这MN对样本里,正样本的预测概率大于负样本的预测概率的个数。注意:这个“预测概率”不一定是真的概率,只要能比大小即可
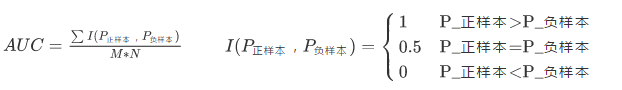
比如现在有2个正例和两个反例:
| ID | label | pro |
|---|---|---|
| A | 0 | 0.1 |
| B | 0 | 0.4 |
| C | 1 | 0.4 |
| D | 1 | 0.8 |
共4种组合:{C,A},{C,B},{D,A},{D,B}.
结果为:$AUC=\frac{1+1+1+0.5}{4}=0.875$
3.用rank法,M个正样本,N个负样本.按照概率排个序,然后将正例的序号相加(重叠取平均),减去常数项,除以常数项即可。
$AUC=\frac{\sum_{ins_i\in{positiveclass}}rank_ins_i-\frac{M\times(M+1)}{2}}{M\times N}$
如:
| ID | label | pro | rank |
|---|---|---|---|
| A | 0 | 0.1 | 1 |
| B | 0 | 0.4 | 2 |
| C | 1 | 0.4 | 3 |
| D | 1 | 0.8 | 4 |
结果:$AUC=\frac{4+(2+3)/2-2\times (2+1)/2}{2\times 2}=0.875$
4.实际使用时直接用别人的实现~
1 | import numpy as np |
3.4 代价敏感错误率与代价曲线
该方法对FN和FP分配了一个代价,😢具体就不做了解了
4 比较检验
照理来说,我们已经学会了评估方法和性能度量,我们应该能够愉快的进行对学习器的优劣比较了。但现实并不像这样简单。对此西瓜书给出了三个因素:
1.我们得到的只是测试集上的性能度量并不能等同于正真的泛化性能。
2.测试集的选择会对结果带来很大的影响。
3.算法本身就有一定的随机性,即使参数相同也会得出不同的结果。
那么我们应该怎么办?(接下来为了方便以错误率ε为例)
首先,我的求得的这个测试样本错误率ε还有没有用?
当然有用,统计假设检验(hypothesis test)为我们提供了重要依据。
假设检验的定义是:在总体的分布函数完全未知或已知其形式,但不知其参数的情况,为了推断总体的某些未知特性,提出某些关于总体的假设。我们要根据样本对所提出的假设作出是接受还是拒绝的决策。
也就是说,我们已经得到了假设,我们需要做的是知道对于这个假设,我们接受的概率是多少,拒绝的概率是多少。很明显当然是接受的概率越高越好,这样才能用我们的这个假设去近似正真情况啊。
那么问题又来了,这个接受概率怎么求?
为此,我们又要推出两个概念:置信度(confidence)=1-α 和 置信区间
比如,在置信度0.95上的置信区间X。意味着真实值落在X上的概率为95%
我们一般都是确定置信度,然后求出相应的置信区间,也就是说我们得将错误率ε变换为一个范围表示。
那么我们的任务变成了怎么将一个数值变成一个范围,并且还要考虑其发生概率?
为此这里将讲述几种西瓜书里提到的检验方法。
4.1 二项检验 binomial test
使用场景:只有一个单独的错误率ε
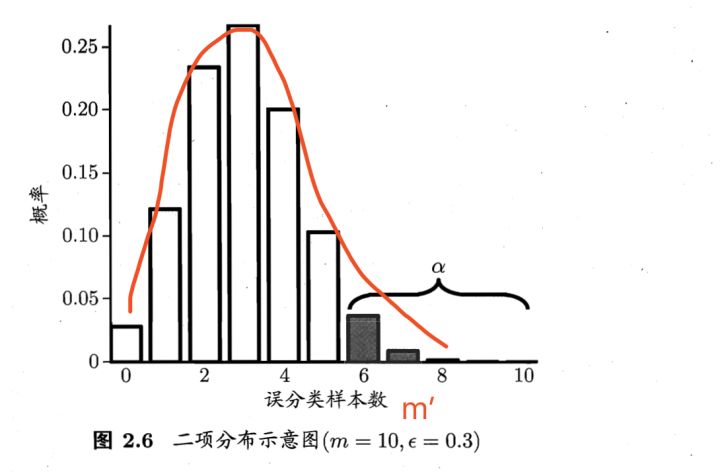
在测试样本m独立采样的条件下,我们可以求出,泛化错误率为ε的学习器被测出测试错误率为ε‘的概率是多少。
$P(\epsilon’;\epsilon)=\epsilon^{\epsilon’\times m}(1-\epsilon)^{m-\epsilon’\times m}$
很明显的,当ε=ε‘时,概率是最大的,而且还符合二项发布。
这时我们假设ε<=ε0,并设置置信度1-α。我们可以求出在这个条件下,测试错误率ε‘。
$\epsilon’=(max \epsilon) s.t (\sum\limits_{i=\epsilon0\times m+1}^{m}\epsilon^i(1-\epsilon)^{m-i})<\alpha (s.t 是 subject to 的缩写,使左边式子在右边条件满足时成立)$
他直接理解就是:在ε0确定的情况下,寻找一个最大的满足右边式子的ε即为ε’。
通俗一点理解就是:因为ε是小于ε0的,因此当误分样本数大于(ε0+m)是不可能的。而我们测出的ε‘满足二项发布,是可能出现误分样本大于(ε0+m)的情况的,于是我们要限制这个情况出现的概率小于某个值α。
实际使用时:我们已经知道了ε’,可以反过来求出当等于α时,相应的ε0为多少。
这样就实现了从一个单独的测试错误率ε‘,转换为一个范围的泛化错误率ε。
4.2 t检验 t-tets
使用场景:有多个错误率的值
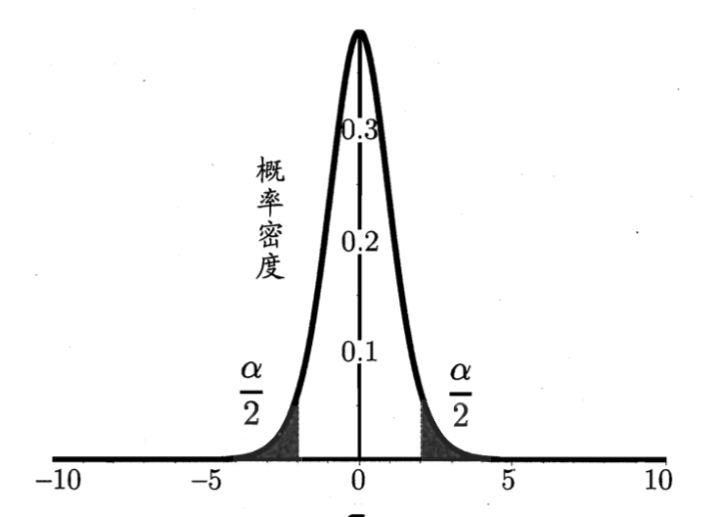
先了解一下什么是t发布:
学生t-分布(Student’s t-distribution)可简称为t分布:
$T=\frac{\overline{X_n}-\mu}{S_n/\sqrt{n}}=\frac{样本均值-整体期望}{样本标准差/\sqrt{样本数}}=n-1自由度的t分布$
T分布,是一种正太分布的近似分布,当自由度趋于无穷时,即为标准正太分布。那为什么不用正太分布呢?因为我们往往得不到正真数据样本的期望和方差,用不了正太,只能用样本的标准差和期望来构建T分布。
所以,T分布用于根据小样本来估计呈正态分布且方差未知的总体的期望。如果总体方差已知(例如在样本数量足够多时),则应该用正态分布来估计总体均值。
1 | from scipy import stats |